0. Intro
로지스틱 회귀분석은 분류 분석에 속하는 분석으로, 종속 변수가 범주형인 경우 새로운 자료에 대한 분류 목적으로 사용한다.
1.1 분류 분석의 유형들
1) 신경망 모형 (Artificial Neural Network)
2) 의사결정나무 (Decision Tree)
3) 앙상블 모형 (Ensenble)
4) 규칙기반 (Rule-Based)
5) 사례기반 (Case-Based)
6) 인접 이웃 (Nearest NEighbor)
7) 베이즈 분류 (Bayesian)
8) 서포트 벡터 머신 (SVM, Support Vector Machine)
9) 유전자 알고리즘
등이 있다.
1. 로지스틱 회귀모형 (Logistic Regression)
반응변수가 범주형인 경우에 적용하는 모형이다. 선형회귀분석이 직접적인 수치를 예측하는 것과 달리 목표변수 y가 특정 범주에 속할 확률 P(Y=i)인 것이다.
즉, 설명변수의 값이 주어질 때 목표변수의 각 범주에 속할 확률이 얼마인지를 추정하여 추정 확률을 기준치에 따라 분류하는 목적으로 사용한다.
모형의 적합을 통해 추정된 확률을 사후확률(Posterior Probability)라고도 한다.
보통 로지스틱 분석에서는 예측하고자 하는 목표변수 y의 범주가 0, 1 두가지가 있다고 가정하고 목표변수 y의 범주가 1이 될 확률 P(Y=1) = P(Y)로 표기하면

위 식의 좌변 P(Y) / { 1 - P(Y) } 를 Odds(오즈)라고 부른다. 즉, Odds는 추정모형에 exp지수함수를 취한 것이다.
좌변은 확률들의 비율이며 우변은 지수함수의 형태이므로, (0 ~ ∞) 의 범위를 가진다. 이에 좌변과 우변 모두 (-∞, ∞)의 범위를 갖게하기 위해 양변에 log를 취하면 두번째 식이 된다.
우변은 선형모델이고 좌변은 log함수이므로 (- ∞, ∞)의 범위를 가진다.
첫 번째 식에서 P(Y)에 대해 정리하면 아래와 같다.

즉, 로지스틱 회귀분석은 주어진 데이터에서 목표변수 Y가 범주값이 1일 확률 (정확히 얘기하자면 범주값이 더 큰 값을 가질 확률)을 위 함수를 이용하여 모형을 쉷하고 모수 β0 β1들을 추정하는 알고리즘이라 할 수 있다.
이러한 모수 β0 β1 추정에는 일반적으로 최대우도추정법(Maximum Likelihood Estimation)을 사용하고, 이는 수식을 변형하는 것 등의 해석학적 방법으로 직접 계산하기 어려우므로 일정 초기값을 부여한 뒤 이를 반복적으로 계산하여 값을 조정해 가는 수치 계산적 방법으로 추정하게 된다.
※ 최대우도추정법 (Maximum Likelihood Estimation)
확률변수 X 의 확률밀도함수 f(X|Θ) 는 Θ 가 상수라는 전제하에서 X 를 변수로 보고 X 가 나타날 확률을 구하는 것이다.
반대로 X 가 이미 정해져 있고 구하려는 모수가 미지의 Θ 값이라고 할 때 이를 우도 함수라고 하고
다음고 같이 정의한다.
L(θ;x)=fX(x|θ)
단지 θ 가 변수이냐 x 가 변수이냐만 다를 뿐이지 같은 개념이고 같은 함수이다.
이 우도 함수를 최대로 하는 θ 값을 θ' 라고 할 때 이 θ' 를 모수 θ 의 최대우도추정량이라고 한다.
즉, 최대 우도 추정(MLE: Maximum Likelihood Estimation) 방법은 주어진 샘플 x에 대해 우도함수값을 가장 크게 해 주는 모수 θ 를 찾는 방법이다.
보통 함수 모형이 주어졌을 때 자연log 를 취해서 곱셈을 덧셈으로 치환한 다음 θ 에 대해 미분을 한 후 값이 0 이 되는 θ 를 찾으면 그것이 최대우도추정량이다.
아래는 로지스틱 함수의 그래프이다. y축은 목표변수 y의 발생확률이므로 0 ~ 1의 값을 가지며, x축은 (- ∞, ∞)의 값을 가진다. 그래프의 모양은 β값에 따라 달라진다. β가 음수(-)이면 그래프가 y축을 기준으로 반대모양이 될 것이다.

따라서, 이항 반응변수 y에 대해 다중 로지스틱 회귀모형의 일반적인 형태는 아래와 같다.
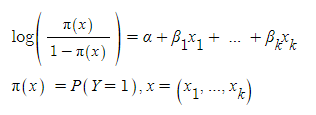
'Data Science > : : Bigdata Analyisis' 카테고리의 다른 글
| 귀무가설, 대립가설 (0) | 2024.04.02 |
|---|---|
| KNN (K-Nearest Neighbor) (0) | 2024.03.11 |
| 데이터로 좋은 결정 내리는 방법, 의사결정 나무 (0) | 2024.03.11 |
| 인공 신경망의 구조 (0) | 2024.03.11 |