0. Intro
KNN이란 k의 개수만큼 주변의 샘플 정보를 이용해서 새로운 관측치의 종속변수(y값)을 예측하는 지도학습
1. KNN (K-Nearest Neighbor)
1.1 KNN (K-Nearest Neighbor) ?

위 그림에서, 빨간색과 파란색의 종속변수의 범주가 있습니다.
일반적으로, 새로운 관측치인 녹색을 분류해야 하는데, 실선으로 k가 3일 때에는 빨강으로, 점선으로 k가 5일 때에는 파란색으로 판별합니다.
가까운 곳에 위치한 것에 따라 가중치(Weight)를 많이 주는 방법도 있습니다.
그리고, KNN은 종속 변수가 어떻게 되는가에 따라 방법이 달라집니다.
범주형 변수의 경우 가장 많이 나타나는 범주로 y를 추정하고, 연속형 변수의 경우 KNN의 평균으로 y를 추정합니다.
중요한 것은, 주변 관측치 정보로 새로운 관측치를 분류 또는 회귀를 하게 되는 것입니다.
2. KNN의 k값은 어떻게 정할까?
KNN은 위 설명처럼 굉장히 직관적이지만, 정해야 할 파라미터도 많습니다. 그 중에서 k를 어떻게 정할지가 제일 중요합니다.
k값
k를 너무 크게 설정하면, 과소적합으로 미세한 경계부분을 잘못 분류할 것이고,
k를 너무 작게 설정하면, 과적합이 되어 이상치의 영향을 크게 받게됩니다.
majority voting
majority voting 시스템, 즉 영역안에 많은 것이 카테고리로 선택되는 시스템을 가지고 있습니다. 기본적으로 특정 카테고리가 많이 포함되어 있다면 잘못 분류가 될 수 있는 것입니다.
예를들면, 남자와 여자 분류에서 남자가 10명, 여자가 100명이라면 KNN을 사용하면 대부분 여자로 예측하게 됩니다.
이러한 문제를 해소하기 위해 k의 크기는 Cross Validation으로 최적의 k를 선정합니다.
majority voting 문제는 거리에 따라 가중치는 방법을 사용합니다.
3. Cross Validation
Cross Validation은 2가지 문제를 해결합니다. (과적합 문제 / 샘플 로스 문제)

위 그림에서 x축은 k의 크기, y축은 error의 크기를 나타내고 있습니다.
Bayes Error(True Error)는 이정도 에러면 가장 적당한 상태라는 것을 나타냅니다.
3.1 과적합 문제
Tran Set에 최적화된 것은 Test Set에 적합하지 않을 수 있습니다. 이는 모델의 복잡도와 밀접한 문제로, 모델이 복잡할수록 과적합이 잘 일어납니다.
위 그림에서 k가 1일 때 train set에 완전 적합하여 error가 나지 않지만, test set에서는 가장 error가 높게 나오고 있습니다. 이럴 때 과적합 문제가 발생했다고 할 수 있습니다.
그래서 k의 크기를 정할 때 test error를 기준으로 가장 error가 낮을 때를 k의 값으로 정하는 것입니다. (위 그림에서는 7정도) 이를 중심으로 왼쪽은 과적합 방향, 오른쪽은 과소적합 방향이라 판단할 수 있습니다.
3.2 샘플 로스 문제
데이터가 많을 때엔 위와 같이 train set, test set으로만 분류하여 정하면 되지만, 데이터가 많지 않을 때엔 train 데이터를 잘 활용해야 합니다.
주어진 데이터를 잘 활용하기 위해 Cross Validation을 사용합니다. 위 그림엔 training / test로 분류하여 일반적인 train 학습만 하면 test error가 Bayes Eroor 선보다 항상 높게 셩성되어 있습니다. 이러한 때에, 아래 그림과 같이 k-fold cross validation을 활용하여 번갈아가며 train 데이터를 충분히 사용하는 것입니다.

4. 가중치 (Weight)
거리를 설명 변수의 종류에 따라 다르게 측정합니다. (nearest neighbors는 가까운 거리를 의미)
4.1 설명 변수가 연속형일 경우
가장 많이 사용하는 것은 유클리디안 거리, 맨하탄 거리입니다.
■ 유클리디안 거리(Euclidian Distance) : 두 점을 가로질러 잇는 직선의 길이
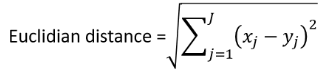

■ 맨하탄 거리 (Manhattan Distance) : 두 점을 잇는 바둑판 길을 따라 가는 길이
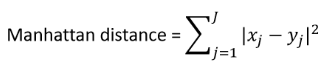
4.2 설명 변수가 범주형일 경우
■ 해밍 거리 (Hamming Distance) : 다른 범주를 다 더하는 것
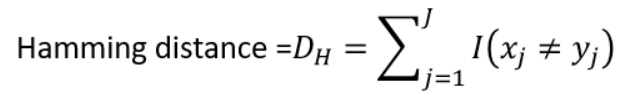
예를들어, 0과 1 범주가 있을 때, 한 점은 '1011101'을, 다른 점은 '1001001'일 때 해밍 거리는 2가 됩니다.
1011101
1001001
여기서 다른 수가 2개라서 (세번째와 다섯번째) 2가 되는 것입니다.
이렇게 구한 거리는 점 (x, y)에 대해 가까운 순서대로 아래와 같이 정렬을 할 수 있고, 여기서 k의 크기를 넣어서 가장 가까운 순서에서 몇번째(k)를 선택하는 것입니다.
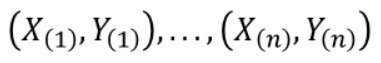
5. KNN의 단점
KNN의 단점은 차원의 영향을 많이 받게 된다는 것입니다. 차원이 높을수록 데이터가 복잡하게 퍼지기 때문에, 거리만으로 판단하면 정확한 예측이 어려워지게 됩니다.
그래서 보통 높은 차원이 있다면, 차원 축소 이후 KNN을 활용하거나, 유의한 변수들만 추려내는 feature selection을 사용합니다.
'Data Science > : : Bigdata Analyisis' 카테고리의 다른 글
| 귀무가설, 대립가설 (0) | 2024.04.02 |
|---|---|
| 로지스틱 회귀분석(Logistic Regression) (0) | 2024.03.27 |
| 데이터로 좋은 결정 내리는 방법, 의사결정 나무 (0) | 2024.03.11 |
| 인공 신경망의 구조 (0) | 2024.03.11 |